‘Root of All Imagination’: Exploring the Complex Root of a Complex Number

Let’s get into some complex fun! and delve into the idea of $√^i{i}$ ... what does that even mean, and/or is such a thing even possible? How can we go about understanding what kind of number i is and how rooting itself with an imaginary base can lead to a real answer (and along the way again a newfound understanding of the concept of rooting)  

Read to find out. Math madness ahoy!!

Before we can get to any sort of proof or deriving, we must first define our terms and concepts so as to prevent confusion and problems.

Let,

1. The number iota (i) be the root of the number negative one, i.e, $i = √^2{-1}$; and any complex number Z ∈ ℂ be expressed in the cartesian form as $Z = a + i·b$ where a, b ∈ ℝ, and in the polar form as $ Z = r(cosθ) + i·r(sinθ) $ where r is the length of the radius from the origin, and $θ = tan^{-1}{|y/x|}$ such that $r↖{→} = x↖{→} + y↖{→}$.
2. The n-th root of a number ω is $√^n{ω}$ where n, ω ∈ ℂ can be represented as $ω^(1/n)$. However ∀ ω ∈ ℂ, $Ϡ$ ∈ ℝ, ω = $a$ + $i·b$ and I(ω)≠0 ∃ $Ϡ$ = $ω^k |√^n{Ϡ}≠(√^n{ω})^{k/2}$.
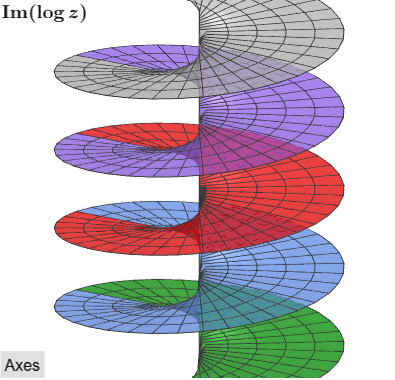
3. The complex logarithm of a nonzero complex number Z (set in any real base β) be a multi-variable function which outputs a set of results varying by a power of ${π/2}$. Thus log$_β$(Z): ℂ* → ℂ
4. r always be equal to 1, i.e., consider here only the real-imaginary unit circle.

To be noted,

• Assumption 3 is justified by the existence of Euler’s identity $e^{iπ} = cosθ + i·sinθ$, which when compared with the equation $Z = r(cosθ) + i·r(sinθ)$ from Assumption 1 can be equated. Thus, $$\table Z, =, re^{iπ}; ln(Z), =, ln(re^{iπ}); ln(Z), =, ln(re^{iπ}); ln(z), =, ln(r) + ln(e^{iπ}); ln(Z), =, ln(r) + iπ,$$ and as we are considering only the unit circle, $r = 1$ (Assumption 4) and consequently $ln(r) = ln(1) = 0$, leading to the natural logarithm of a complex number be represented as $ln(Z) = i·θ$.

• $e^{iθ} = cosθ + i·sinθ$; so when $θ = π$, $e^{iπ} = cos(π) + i·sin(π)$. Therefore, $$\table e^{iπ}, =, cos(π) + i·sin(π); e^{iπ}, =, -1 + i(0); e^{iπ}, =, -1 + 0; e^{iπ} + 1, =, 0$$

Consider, now, $θ=nπ/2$, n ∈ {{1} + {4ℕ+1}}. And as n ∈ {{1} + {4ℕ+1}}, $i^n$ will always equal to iota itself, i.e, $i^n = i$ ∀ n ∈ {1, 5, 9, 13, …}

Then, let ① be, $$ e^{iθ} = e^{i(nπ/2)}$$

Since $$\table e^{iπ} + 1, =, 0; e^{iπ}, =, -1; √^2{e^{iπ}}, =, √^2{-1}; e^{i(π/2)}, =, i$$

Applying this knowledge in ①, we get ② (the final statement), $$\table e^{i(nπ/2)}, =, (e^{i(π/2)})^n; e^{i(nπ/2)}, =, i^n; e^{i(nπ/2)}, =, i$$

Thus, we get ③, $$ln(i) = i·nπ/2$$

Moving forward from the note made about the natural log of Z, with $Z = e^{i(nπ/2)}$ and taking into consideration ②, we get $$\table e^{i(nπ/2)}, =, i; ln(e^{i(nπ/2)}), =, ln(i); log_e(e^{i(nπ/2)}), =, log_e(i)$$ 

Extrapolating from Assumption 2, we have, $$\table √^i{i}, =, i^(1/i); , =, e^{ln(i^(1/i))}; , =, e^{{1/i}ln(i)}$$ Substiting with ③, $$\table √^i{i} = e^{{1/i}(inπ/2)}$$ Finally, we get ④, the answer to the question we had set out to find, $$ √^i{i} = e^{nπ/2}$$

Therefore, we find that $√^i{i}$ ∈ ℝ, and that

$√^i{i} = e^{nπ/2}$, n ∈ {{1} + {4ℕ+1}}

Finding values of $√^i{i}$ with values of e and π accurate to 10 decimal points, $$(\table e, ≈, 2.7182818284;π, ≈, 3.1415926535;)$$

With these prescribed values, the value of 

$\table e^{π/2}, =, 2.7182818284^(3.1415926535/2); , =, 2.7182818284^1.5707963267; , =, 4.8104773803$

Value Table of $√^i{i}$

$(\table Sno.,, n,, equation,, value; 1,, 1,, e^{1π/2},, 4.8104773803; 2,, 5,, e^{5π/2},, 2575.9704948161; 3,, 9,, e^{9π/2} ,, 1379410.7040888692; 4,, 13,, e^{13π/2},, 738662921.1724631606; 5,, 17,, e^{17π/2},, 395547830314.5634311430; 6,, 21,, e^{21π/2},, 211812562377188.5543251283; 7,, 25,,e^{25π/2},, 113423859625551210.2855772693; 8,, 29,, e^{29π/2},, 60737530333291774625.9199454398; 9,, 33,, e^{33π/2},, 32524440652665813611023.2290910428; 10,, 37,, e^{37π/2},, 17416566560477224523726469.0135233006; ⋮,, ⋮,, ⋮,, ⋮)$

(As you can see, all values and answers have been kept accurate till 10 decimal values—at least I have tried to do so. There is not enough character space for the final two values in the output table and they get shortened automatically on the right by the jqMath, which I'm using. Additionally, certain devices seem to have issues displaying the table matrix properly. For the sake of records, the values of  $√^i{i}$ accurate up to 10 decimal digits are listed below.)

Hence, $√^i{i}$ ≈ {4.8104773803, 2575.9704948161, 1379410.7040888692, 738662921.1724631606, 395547830314.5634311430, 211812562377188.5543251283, 113423859625551210.2855772693, 60737530333291774625.9199454398, 32524440652665813611023.2290910428, 17416566560477224523726469.0135233006…}

PLEASE NOTE: The correct value of $√^i{i}$ is only the principal value due to DeMoivre's Theorem, from which we understand that $$\table z^n, = , [cos(θ) + i.sin(θ)]^n;  e^{iπ}^n,=, [cos(θ) + i.sin(θ)]^n; e^{i(nπ)}, =, [cos(θ) + i.sin(θ)]^n; [cos(θ) + i.sin(θ)]^n, =, [cos(nθ) + i.sin(nθ)];$$Thus, there is no merit in the values beyond the first one. However, I still think there is some value and understanding gained by taking a generalised approach that would not be otherwise, that is, if we only took the smallest natural number that could work with the given conditions instead of seeing the larger patterns at play.

Post-Proof Points:

• It should be noted that saying that $√^i{i} = e^{π/2}$ (considering only the principal value, here) is not similar to creating a value $Ϡ$ as stated in Assumption 2 and then finding the root of the k-th root of $Ϡ$. Such would have been the case iota were to have been biquadrated and then the 4th root be taken before taking the root of that resultant Real Number. Although the final value of $√^i{i}$ is a set of Real Numbers, it does not originate from a $Ϡ$-transformation as it is the interpretation of the i-th root itself that is being changed and not the value of i inside the root. For Complex but non i-th roots of i, the resultant value is still a Complex Number.
• The m-th root of a number k, where m ∈ ℝ $$⇓$$ $$∏↙{j = 1}↖{m} √^m{k} = k$$ However, this is only a primary understanding of the root function. This is similar to how the basic idea that trigonometry is about right-angled triangled breaks down for obtuse-angled triangles and further ($sin(θ)$ and $cos(θ)$ exist for θ ∈ [$π/2$, $2π$]) such that we have to redefine trigonometry in terms of circles, the unit circle to be exact and the triangles inscribed within it. Similarly, the notion that the root of a function can be defined in terms of $∏↙{j = 1}↖{m} √^m{k} = k$ only when m is a Real Number. For situations where m ∈ ℂ and I(m)≠0, the root function is a property of reciprocal powers of m applied to k where $$√^m{k} ⇒ k^{(1/m)m} = k$$ and $$√^m{k} ⇏ ∏↙{j = 1}↖{m} √^m{k} = k$$ and that the prior interpretation of √^m{k}$ is only a case scenario.
• To further showcase the previous points, $$√^i{i} = e^{π/2}$$ $$⇓$$ $$e^{iπ/2} = (e^{iπ})^{1/2} = √^2{e^{iπ}} = √^2{-1} = i$$ This holds true when we interpret θ to repeat after ever 2π rad like with the unit circle or a phasor diagram. This may call into question the validity of having $√^i{i}$ equal to an infinitely long set of ever-increasing values. To be honest, I’m not sure myself. Generally, with such proofs for complex numbers like $i^i$ we restrict ourselves to merely the primary value, so the reader is also free to restrict the answer to its principal value if they so please.
• Another illegal $Ϡ$-transformation would have been if we defined a $Ϡ = i^2 = √^2{e^{iπ}}$ such that we could then (incorrectly) state, $$\table √^i{i}, =, √^i{√^2{e^{iπ}}}; ,=, (e^{iπ})^(1/{2i}); , =, (e^{-π/2}); , =, (1/e)^{π/2}$$